Intensité énergétique (physique)

Intensité énergétique

L'intensité énergétique mesure l'énergie électromagnétique transférée dans une direction donnée.

Données clés

Unités SI	watt par stéradian
Base SI	kg m2 s−3
Nature	Distribution angulaire extensive
Symbole usuel	$I_{\mathrm {e} }$
Lien à d'autres grandeurs	$I_{v}$ = $K_{m}$ $I_{e}$ $\mathrm {d} I_{\mathrm {e} }$ = $L_{\mathrm {e} }$ $\cos \theta \,\mathrm {d} S$

L’intensité énergétique est une grandeur radiométrique qui est la mesure de la puissance (ou flux énergétique) d'un rayonnement électromagnétique émise par une source quasi-ponctuelle, par unité d'angle solide, dans une direction donnée. Son unité dans le Système international d'unités est le watt par stéradian (W sr⁻¹).

Cette grandeur sert à définir la candela, l'unité de mesure de son correspondant photométrique l'intensité lumineuse.

Définitions

L'intensité énergétique est obtenue par intégration sur une surface $\Sigma ({\vec {r}})$ donnée de la luminance $L_{e}({\vec {r}},{\vec {\Omega }})$ dans le cône $\mathrm {d} \Omega$ autour de la direction ${\vec {\Omega }}_{0}$ :

$I_{e}({\vec {\Omega _{0}}})=\int _{\Sigma }L_{e}({\vec {r}},{\vec {\Omega }}_{0})\,{\vec {\Omega }}_{0}\cdot {\vec {n}}({\vec {r}})\,\mathrm {d} \Sigma$

${\vec {r}}$ désigne la variable d'espace et ${\vec {n}}$ la normale locale à la surface $\Sigma$.

C'est donc la puissance par unité d'angle solide émise dans la direction ${\vec {\Omega }}_{0}$ par un faisceau dont la taille est celle de la surface émettrice.

Cette notion sert généralement pour étudier les phénomènes lointains, c'est-à-dire lorsque la distance à la source est grande par rapport à la taille de celle-ci, sous réserve d'une régularité angulaire de la luminance (pas de variation notable pour un faible écart angulaire). On parle alors de source quasi-ponctuelle (et non de source ponctuelle car cette dernière correspondrait à une luminance infinie).

Un cas particulier est celui d'une surface homogène générant un rayonnement isotrope. Dans ce cas $L_{e}({\vec {r}},{\vec {\Omega }}_{0})=L_{0}$ et

$I_{e}({\vec {\Omega _{0}}})=A\,L_{0}\,,\quad A=\int _{S}{\vec {\Omega }}_{0}\cdot {\vec {n}}\,\mathrm {d} S$

A est l'aire de la surface projetée sur un plan perpendiculaire à ${\vec {\Omega }}_{0}$. Ceci suppose l'absence de parties cachées et donc une surface convexe de forme quelconque.

Relations entre intensité énergétique et flux énergétique

Pour une source donnée $L_{e}({\vec {r}},{\vec {\Omega }}_{0})$ on peut écrire le flux énergétique pour la luminance énergétique $L_{e}({\vec {r}},{\vec {\Omega }}_{0})$ en fonction de $I_{e}({\vec {\Omega _{0}}})$ par simple permutation des signes somme :

${\begin{array}{rcl}\Phi _{e}&=&\int _{\Sigma }\int _{S^{2}}L_{e}({\vec {r}},{\vec {\Omega }}_{0})\,{\vec {\Omega }}_{0}\cdot {\vec {n}}({\vec {r}})\,\mathrm {d} \Omega \,\mathrm {d} \Sigma \\[0.6em]&=&\int _{S^{2}}\int _{\Sigma }L_{e}({\vec {r}},{\vec {\Omega }}_{0})\,{\vec {\Omega }}_{0}\cdot {\vec {n}}({\vec {r}})\,\mathrm {d} \Sigma \,\mathrm {d} \Omega \\[0.6em]&=&\int _{S^{2}}I_{e}({\vec {\Omega }}_{0})\,\mathrm {d} \Omega \end{array}}$

$\Phi _{e}$ est un scalaire qui est le résultat d'une intégration sur un angle solide fini et ne dépend donc pas de $\Omega _{0}$. Corrélativement il existe donc une infinité d'intensités qui donnent un même flux.

Dans le cas particulier d'une intensité constante $I_{0}$ on a :

$\Phi _{0}=I_{0}\int _{S^{2}}\mathrm {d} \Omega =4\pi I_{0}$

On trouve dans certaines références les expressions $\mathrm {d} \Phi _{e}=I_{e}\mathrm {d} \Omega$ ou $I_{e}={\frac {\mathrm {d} \Phi _{e}}{\mathrm {d} \Omega }}$ voire $I_{e}={\frac {\partial \Phi _{e}}{\partial \Omega }}$ qui n'ont pas de sens mathématique car $I_{e}({\vec {\Omega }}_{0})$ est une distribution et $\mathrm {d} \Omega$ et $\mathrm {d} \Phi _{e}$ des scalaires : elles sont donc inhomogènes. Elles supposent implicitement et parfois explicitement que l'on peut calculer l'intensité à partir du flux, ce qui constitue un non-sens.

Unités

L'unité est le watt par stéradian (W sr⁻¹) lorsque l'intensité énergétique est relative à l'ensemble du spectre.

L'intensité énergétique spectrale est une distribution statistique $I_{p}$ de l'intensité relative à un intervalle du spectre mesuré par la quantité $p$ (fréquence, longueur d'onde, nombre d'onde, énergie, etc.). L'unité correspondante sera donc le $\mathrm {W\,sr^{-1}\,p^{-1}}$. Sa valeur numérique est dépendante du choix de $p$ mais $I_{p}\mathrm {d} p$ ne dépend pas du choix effectué : cela représente l'intensité dans l'intervalle $\mathrm {d} p$.

Mesure

Diagramme de rayonnement d'une antenne.

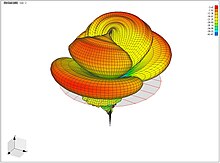
La mesure est une opération complexe puisqu'elle doit être faite à une distance suffisante, couvrir toute la sphère (ou au moins la partie intéressante de celle-ci) et éventuellement tout le spectre du rayonnement.

La représentation graphique d'une telle mesure est un diagramme de rayonnement.

Articles connexes

• Radiométrie
• Intensité lumineuse | Candela
• Éclairement énergétique

Bibliographie

• Le Système international d'unités (SI), Sèvres, Bureau international des poids et mesures, 2019, 9^e éd., 216 p. (ISBN 978-92-822-2272-0, lire en ligne [PDF])
• Tamer Bécherrawy, Optique géométrique : cours et exercices corrigés, Bruxelles, De Boeck Université, 2006, 402 p. (ISBN 2-8041-4912-9, lire en ligne)